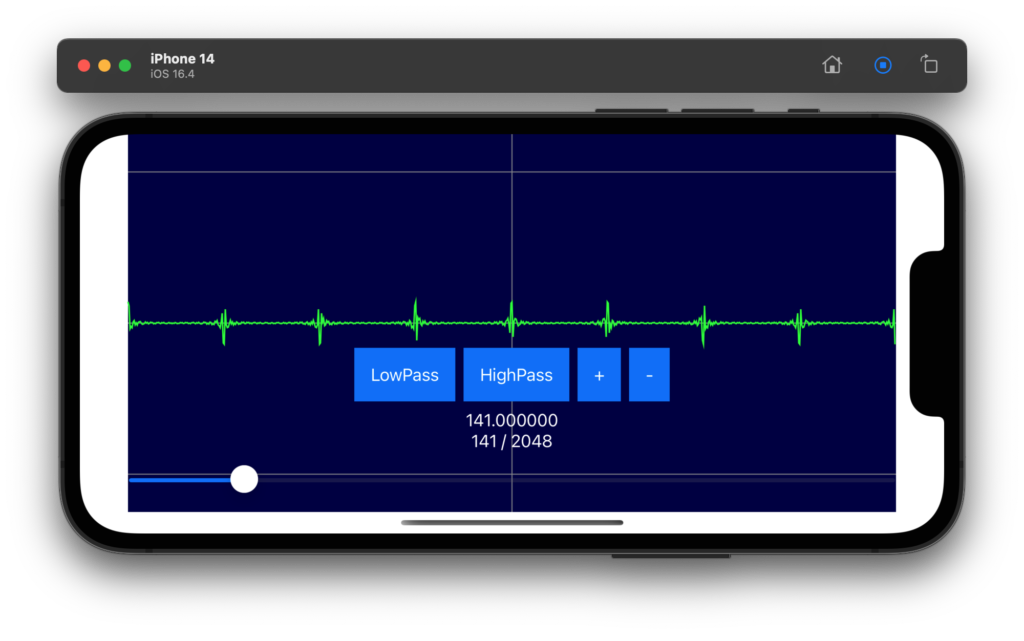
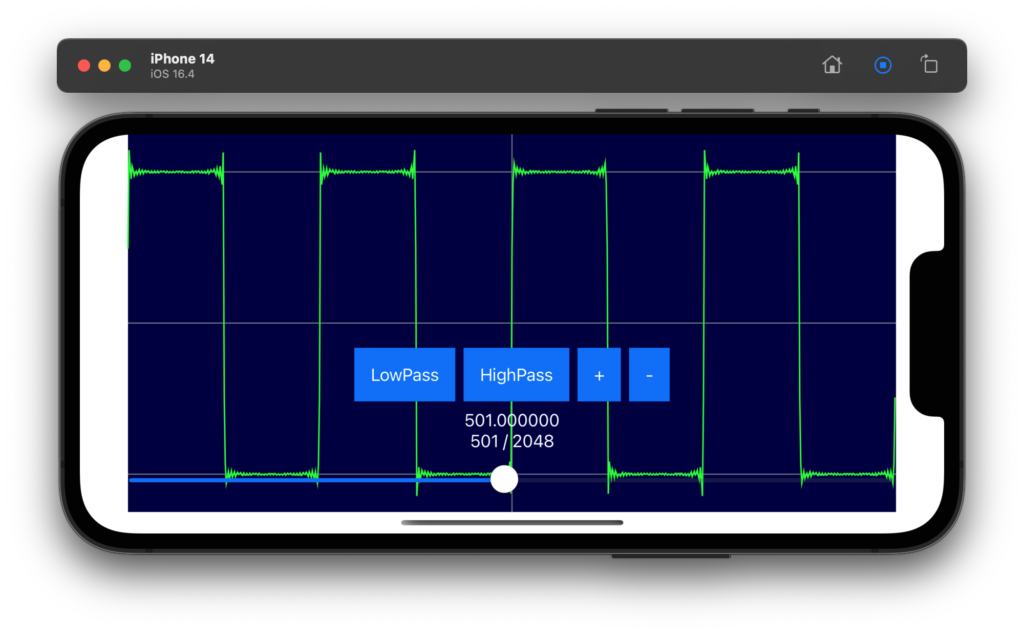
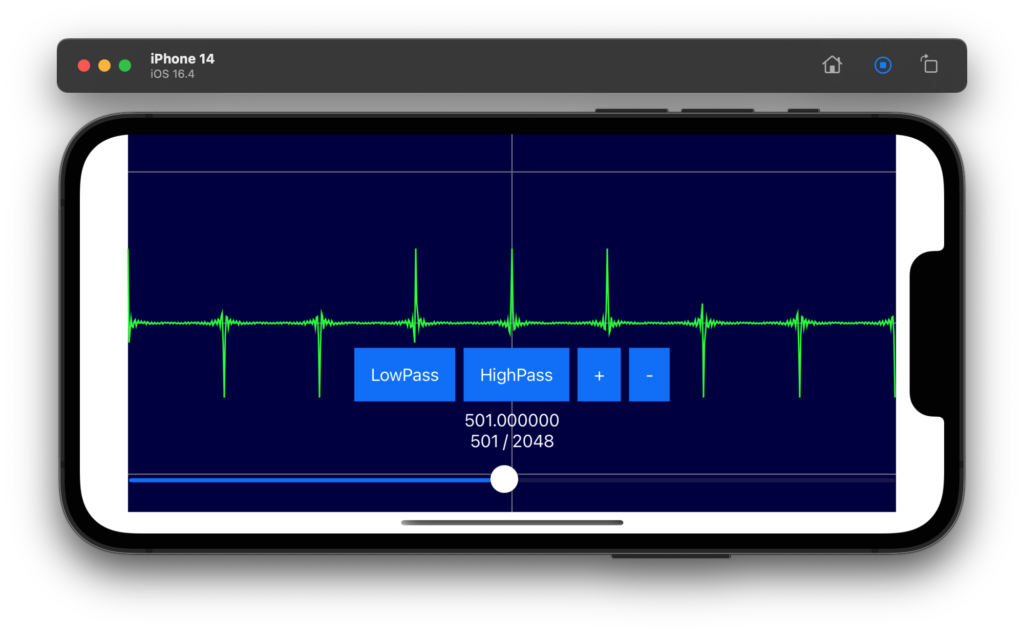
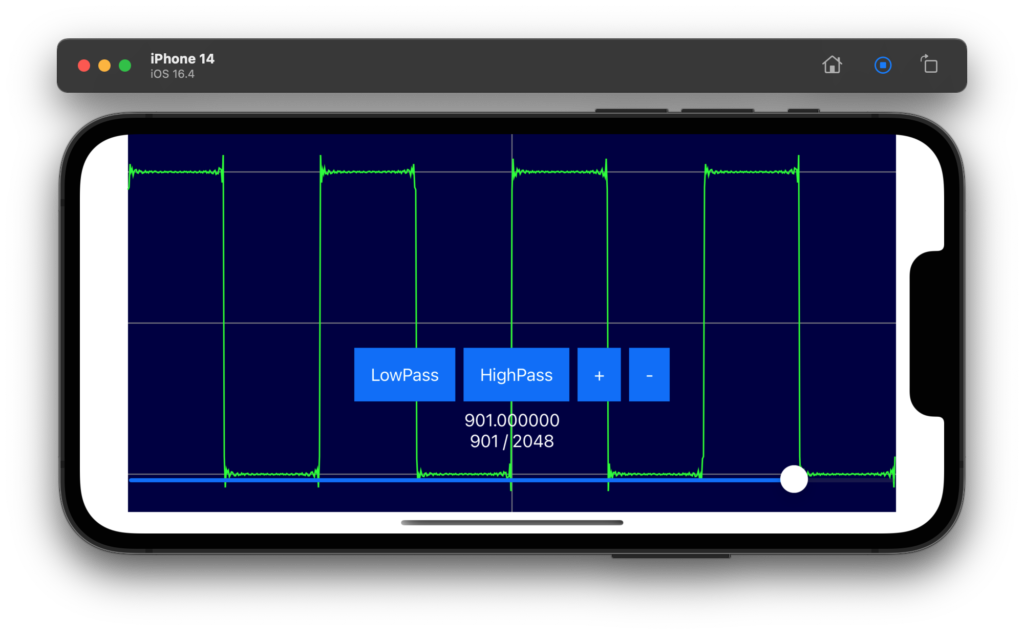
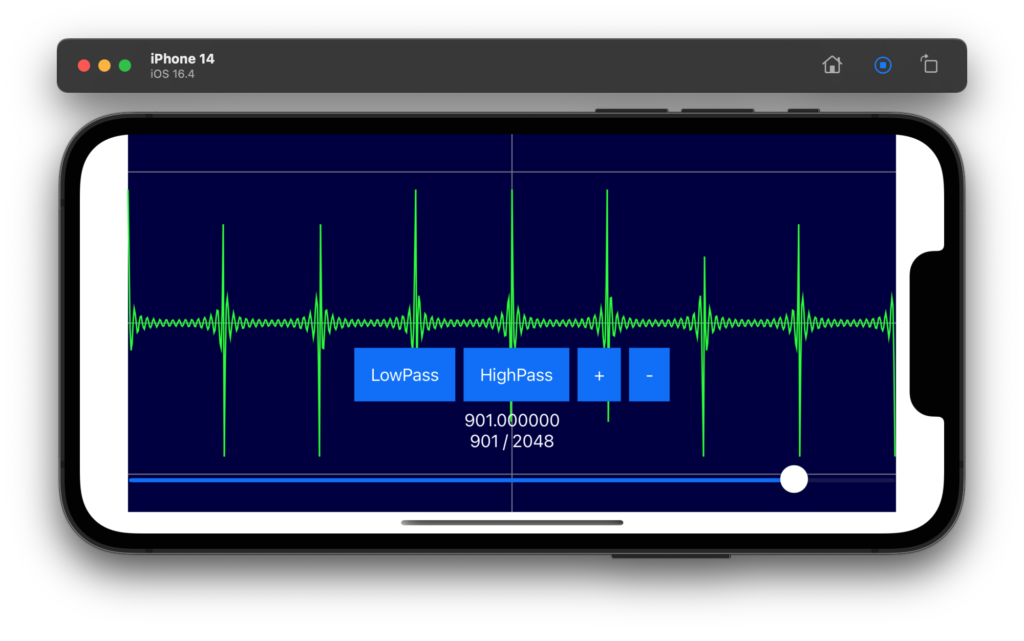
高速フーリエ変換を実施する(独自コード)
iPhone や Mac などでフーリエ変換などを実施する場合は、Apple社が Accelerate フレームワークという信号処理用の高速なライブラリを用意してくれているので、それを使うのがいいです。
といいつつ、以前、C言語で書いた独自のコードがあるので、それを Swift に翻訳してみました。車輪の再発明といわれても気にしません(笑)。
import SwiftUI
// データ配列の要素をなす構造体の型.
struct X_FX {
var x: Double
var fx: Double
}
// スライダ用の定数.
struct SLIDER {
static let MIN: Double = 0.0
static let MAX: Double = 1022.0
static let STEP: Double = 1.0
}
struct ContentView: View {
// 背景の色と波形の色.
let COLOR_BG = Color( red: 0.0, green: 0.0, blue: 0.3, opacity: 1.0 )
let COLOR_WAVE = Color( red: 0.0, green: 1.0, blue: 0.0, opacity: 1.0 )
// データの配列.
let NUM_DATA = 2048
@State var Data: [X_FX] = []
// フーリエ変換オブジェクト.
let Fourier = MyFourierObject()
// スライダと関係するフィルタリングの次数.
@State var SliderValue: Double = 60.0
@State var Threshold = 60
// ローパスフィルタリングするかハイパスフィルタリングするか.
@State var ModePassLow: Bool = true
// f(x) 方向の描画倍率
let DRAW_RATE = 0.8
var body: some View {
GeometryReader {
geom in
ZStack{
// 画面のうち ZStack が占めるサイズ.
let RectW = geom.size.width
let RectH = geom.size.height
// 波形描画の背景の矩形を描画する.
Rectangle()
.foregroundColor( COLOR_BG )
.frame( width: RectW, height: RectH )
// 目安になるセンター十字線と振幅の高さを描画する.
Path{ path in
let plot_x = RectW * 0.5
let plot_y = RectH * 0.5
// センターの垂直線.
let pnt00 = CGPoint( x: plot_x, y: 0 )
let pnt01 = CGPoint( x: plot_x, y: RectH )
path.move( to: pnt00 )
path.addLine( to: pnt01 )
// センターの水平線.
let pnt10 = CGPoint( x: 0, y: plot_y )
let pnt11 = CGPoint( x: RectW, y: plot_y )
path.move( to: pnt10 )
path.addLine( to: pnt11 )
// 振幅 f(x) のプラス側のめやす水平線.
let tmp0 = ( plot_y - ( plot_y * DRAW_RATE ))
let pnt20 = CGPoint( x: 0, y: tmp0 )
let pnt21 = CGPoint( x: RectW, y: tmp0 )
path.move( to: pnt20 )
path.addLine( to: pnt21 )
// 振幅 f(x) のプラス側のめやす水平線.
let tmp1 = ( plot_y + ( plot_y * DRAW_RATE ))
let pnt30 = CGPoint( x: 0, y: tmp1 )
let pnt31 = CGPoint( x: RectW, y: tmp1 )
path.move( to: pnt30 )
path.addLine( to: pnt31 )
}
.stroke( .gray, lineWidth: 1.0 )
.frame( width: RectW, height: RectH ) // ここが重要.
// 波形を描画する.
Path{ path in
let amp = RectH * 0.5 * DRAW_RATE
let off_y = RectH * 0.5
if ( Data.count > 0 )
{
var plot_x = Double(0)
var plot_y = -( Data[0].fx ) * amp + off_y
var pnt = CGPoint( x: plot_x, y: plot_y )
path.move( to: pnt )
let loop = Int( RectW )
for i in 1 ..< loop {
let rate = Double(i)/Double( RectW - 1 )
let n = Int( rate * Double( Data.count - 1 ))
plot_x = Double(i)
plot_y = -( Data[n].fx ) * amp + off_y
pnt = CGPoint( x: plot_x, y: plot_y )
path.addLine( to: pnt )
}
}
}
.stroke( COLOR_WAVE, lineWidth: 1.5 )
.frame( width: RectW, height: RectH ) // ここが重要.
VStack{
// データをセットするボタンを水平に並べる.
HStack{
// ローパスフィルタを選択するボタン.
Button( action: {
ModePassLow = true
processing( &Data, NUM_DATA, Threshold, ModePassLow )
}){
Text( "LowPass" )
.foregroundColor( .white )
}
.padding()
.background( .blue )
// ハイパスフィルタを選択するボタン.
Button( action: {
ModePassLow = false
processing( &Data, NUM_DATA, Threshold, ModePassLow )
}){
Text( "HighPass" )
.foregroundColor( .white )
}
.padding()
.background( .blue )
// フィルタ次数をひとつ増加するボタン.
Button( action: {
SliderValue += 1
if SliderValue > SLIDER.MAX
{
SliderValue = SLIDER.MAX
}
Threshold = Int( SliderValue )
processing( &Data, NUM_DATA, Threshold, ModePassLow )
}){
Text( "+" )
.foregroundColor( .white )
}
.padding()
.background( .blue )
// フィルタ次数をひとつ減らすボタン.
Button( action: {
SliderValue -= 1
if SliderValue < SLIDER.MIN
{
SliderValue = SLIDER.MIN
}
Threshold = Int( SliderValue )
processing( &Data, NUM_DATA, Threshold, ModePassLow )
}){
Text( "-" )
.foregroundColor( .white )
}
.padding()
.background( .blue )
}
// スライダの値を示す.
Text( String( format: "%f", SliderValue ) )
.foregroundColor( .white )
// フィルタ次数の値を示す.
Text( String( format: "%d / %d", Threshold, NUM_DATA ) )
.foregroundColor( .white )
// フィルタ次数を決定するスライダ.
Slider(
value: $SliderValue,
in: SLIDER.MIN...SLIDER.MAX,
step: SLIDER.STEP,
onEditingChanged: {
editing in
// これをコメントインしてもなんだか違いがわからない.
//Threshold = Int( SliderValue )
//processing( &Data, NUM_DATA, Threshold, ModePassLow )
}
).onChange( of: SliderValue ){ new_value in
Threshold = Int( new_value )
processing( &Data, NUM_DATA, Threshold, ModePassLow )
}
}
.frame( maxWidth: .infinity, maxHeight: .infinity, alignment: .bottom )
.padding( .bottom )
}
.onAppear(){
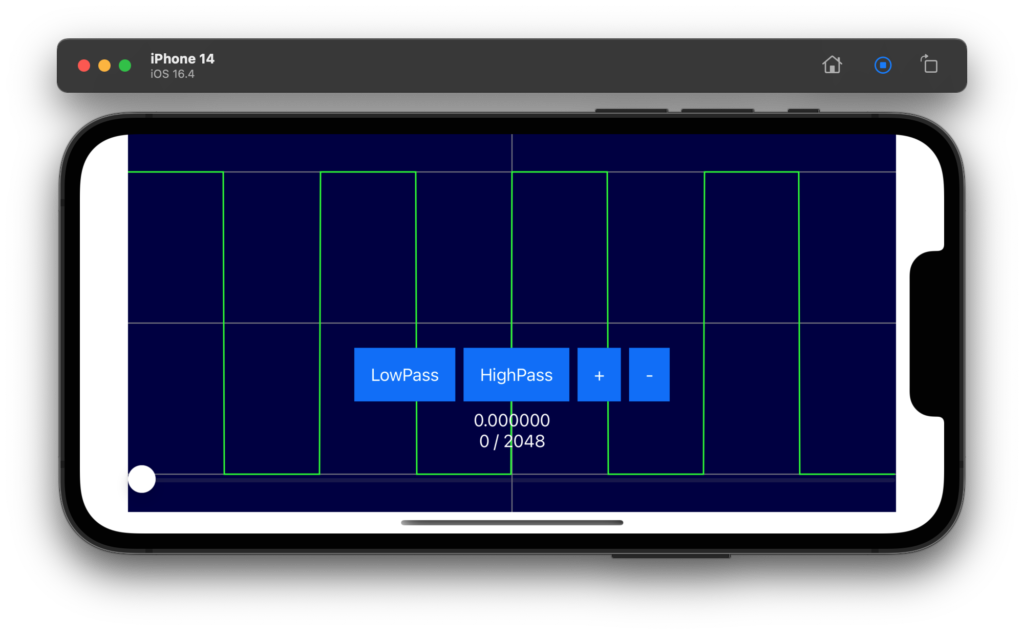
// 起動時に矩形波データを仕込む.
SetDataSquare( &Data, NUM_DATA )
}
}
}
// フーリエ変換して周波数領域でフィルタリングして逆フーリエ変換する.
func processing( _ data: inout[X_FX], _ num_data: Int, _ threshold: Int, _ mode_filter: Bool )->Void
{
// 矩形波を仕込む.
let _ = SetDataSquare( &data, num_data )
// 実部と虚部のデータ領域を確保する.
var data_re = [Double]( repeating: 0.0, count: num_data )
var data_im = [Double]( repeating: 0.0, count: num_data )
// f(x) のデータを実部に仕込み、虚部に 0.0 を仕込む.
for n in 0 ..< num_data
{
data_re[n] = data[n].fx
data_im[n] = 0.0
}
var mode = 0
// フーリエ変換.
mode = MyFourierObject.MODE_TIME_TO_FREQ
let _ = Fourier.Transform( mode, &data_re, &data_im )
// 周波数領域でフィルタリングを実施する.
if ( mode_filter )
{
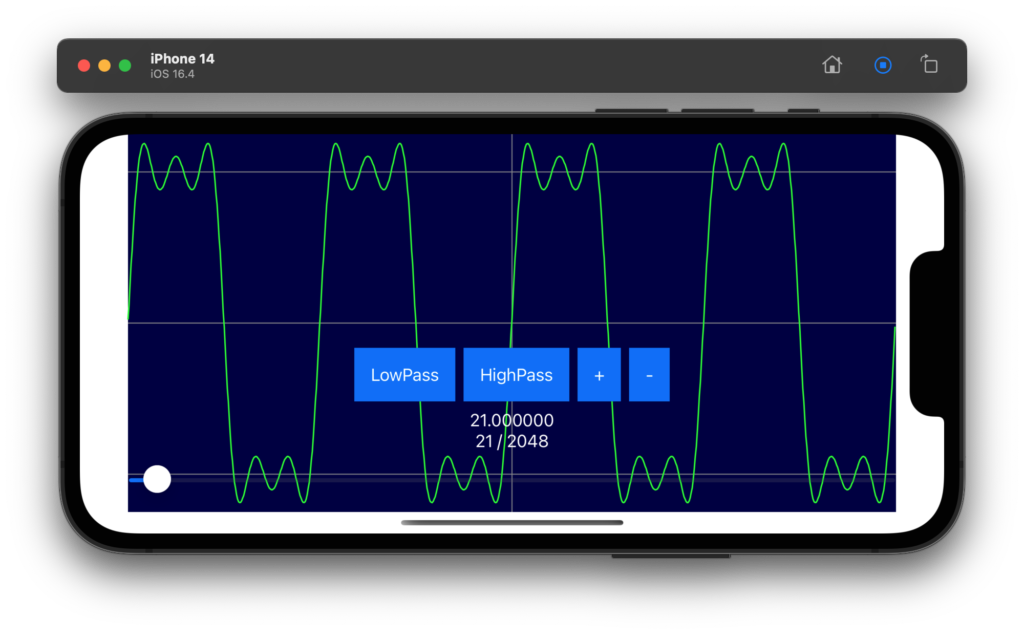
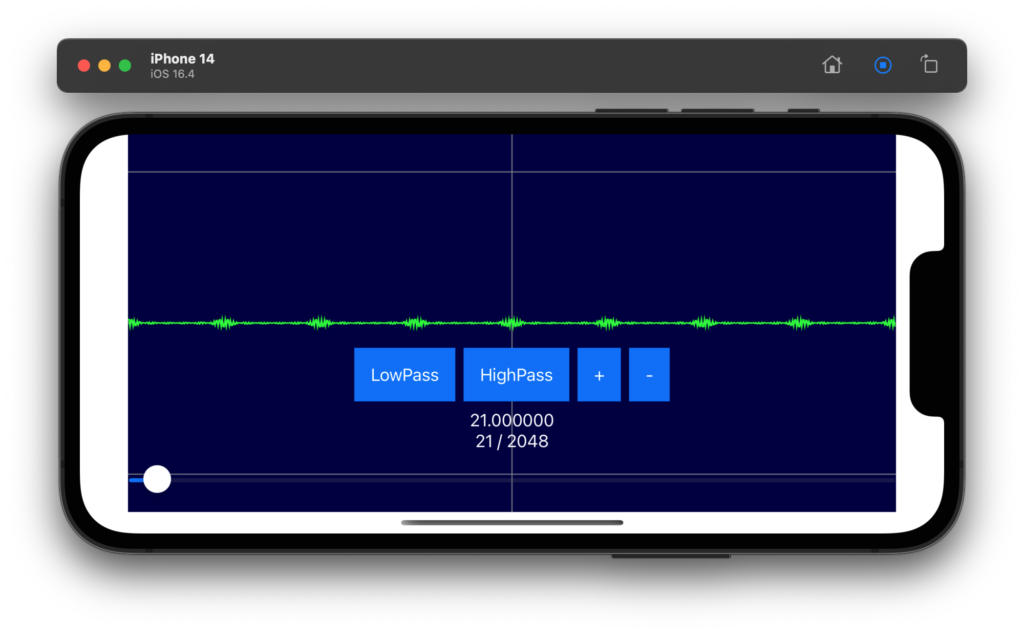
// ローパスフィルタ.
let _ = FilteringPassLow( &data_re, &data_im, num_data, threshold )
}
else
{
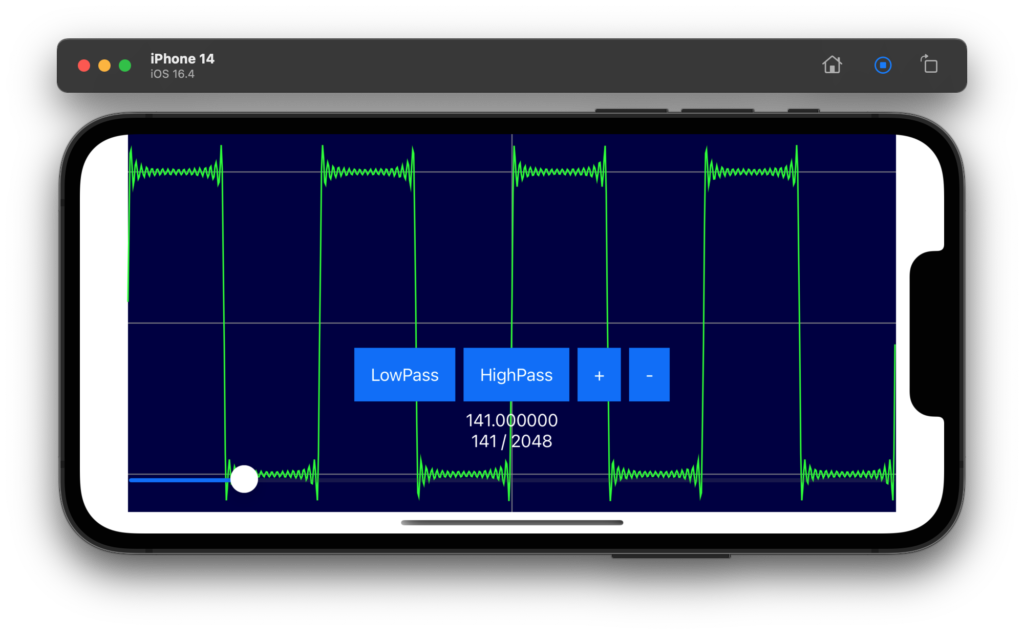
// ハイパスフィルタ.
let _ = FilteringPassHigh( &data_re, &data_im, num_data, threshold )
}
// フーリエ逆変換.
mode = MyFourierObject.MODE_FREQ_TO_TIME
let _ = Fourier.Transform( mode, &data_re, &data_im )
// 実部のデータだけを元のデータ f(x) に書き戻す.虚部のデータはすべて 0.0 前後の値である.
for n in 0 ..< num_data
{
data[n].fx = data_re[n]
}
return
}
// サイン波形を格納する.
func SetDataSin( _ data: inout [X_FX], _ req_num_data: Int )->Void {
// いったん配列をクリアする.
data.removeAll()
let RANGE = 2.0
let MUL = 2.0
for n in 0 ..< req_num_data {
let rate = Double(n)/Double( req_num_data - 1)
var v = RANGE * rate
v -= 1.0 // この時点で -1.0 〜 0.0 〜 +1.0 になる.
let t = v * ( 2.0 * ( Double.pi )) * MUL
let ft = sin( t )
// データ要素を追加する.
let element = X_FX( x: t, fx: ft )
data.append( element )
}
}
// 矩形波を格納する.
func SetDataSquare( _ data: inout [X_FX], _ req_num_data: Int )->Void {
// いったん配列をクリアする.
data.removeAll()
// サイン波形をしこむ.
SetDataSin( &data, req_num_data )
// サイン波形の正負を評価して、矩形波をつくる.
for n in 0 ..< req_num_data {
if ( data[n].fx >= 0.0 )
{
data[n].fx = +1.0;
}
else
{
data[n].fx = -1.0
}
}
}
// ローパスフィルタリングを実施する.
func FilteringPassLow( _ data_re: inout [Double], _ data_im: inout [Double], _ num_data: Int, _ threshold: Int )->Bool{
let beg = threshold
let fin = num_data - threshold
if ( beg < 0 ){ return false }
if ( beg >= num_data ) { return false }
if ( fin < 0 ){ return false }
if ( fin >= num_data ) { return false }
for k in beg ... fin
{
data_re[k] = 0.0
data_im[k] = 0.0
}
return true
}
// ハイパスフィルタリングを実施する.
func FilteringPassHigh( _ data_re: inout [Double], _ data_im: inout [Double], _ num_data: Int, _ threshold: Int )->Bool{
let half = num_data >> 1
let beg = half - threshold
let fin = half + threshold
if ( beg < 0 ){ return false }
if ( beg >= num_data ) { return false }
if ( fin < 0 ){ return false }
if ( fin >= num_data ) { return false }
var a = 0
var b = 0
a = 0
b = beg
for k in a ..< b
{
data_re[k] = 0.0
data_im[k] = 0.0
}
a = fin + 1
b = num_data - 1
for k in a ..< b
{
data_re[k] = 0.0
data_im[k] = 0.0
}
return true
}
}
struct ContentView_Previews: PreviewProvider {
static var previews: some View {
ContentView()
}
}
下記がC言語で書いたものを Swift に翻訳したライブラリです。ほとんど何も考えなくてもC言語から翻訳できましたが、for 文の翻訳だけは難しいのでC言語のコメントアウトを残しておきます。
本記事をご覧の皆様はご存知でしょうが、データの個数は 2 のべき乗で実行してください。
最近は2のべき乗でなくても適用できる高速フーリエ変換のアルゴリズムがあるそうですね。Generalized FFT とか インテルの MKL-FFT とかそういうやつです。私はなんのことやらサッパリわかりませんが、頭のいい人はたくさんいるのですね。
import Foundation
public class MyFourierObject{
public static let MODE_TIME_TO_FREQ = +1;
public static let MODE_FREQ_TO_TIME = -1;
public init(){
}
private func bit_reverse( _ data: inout [Double] )->Int
{
if ( data.count <= 1 )
{
return -1;
}
let num_data = data.count
var i: Int = 0
var k: Int
var tmp: Double
i = 0;
// for ( int j = 1; j < num_data - 1; j++ )
for j in 1 ..< num_data - 1
{
k = num_data >> 1;
while( k <= i )
{
i = i - k;
k = k >> 1;
}
i = i + k;
if ( j < i )
{
tmp = data[j];
data[j] = data[i];
data[i] = tmp;
}
}
return 0;
}
public func Transform( _ mode: Int, _ data_re: inout [Double], _ data_im: inout [Double] )->Int
{
if ( data_re.count != data_im.count )
{
return -1
}
if ( data_re.count <= 1 )
{
return -1
}
if ( !(( mode == MyFourierObject.MODE_TIME_TO_FREQ ) || ( mode == MyFourierObject.MODE_FREQ_TO_TIME )) )
{
// for ( int n = 0; n < data_re.count; n++ )
for n in 0 ..< data_re.count
{
data_re[n] = 0.0
data_im[n] = 0.0
}
return -1
}
let num_data = data_re.count;
var tmpReJ: Double;
var tmpImJ: Double;
var tmpReK: Double;
var tmpImK: Double;
var newReJ: Double;
var newImJ: Double;
var newReK: Double;
var newImK: Double;
var k: Int;
var n_half: Int;
var n_half2: Int;
var cos_tbl = [Double]( repeating: 0.0, count: num_data )
var sin_tbl = [Double]( repeating: 0.0, count: num_data )
var arg: Double;
let PAI = Double.pi;
let PAI_TWICE = PAI * 2.0;
if ( mode > 0 )
{
// for ( int n = 0; n < num_data; n++ )
for n in 0 ..< num_data
{
arg = (Double)( -( PAI_TWICE * Double(n) ) )/(Double)( num_data );
cos_tbl[n] = cos( arg );
sin_tbl[n] = sin( arg );
}
}
else
{
// for ( int n = 0; n < num_data; n++ )
for n in 0 ..< num_data
{
arg = (Double)( +( PAI_TWICE * Double(n) ) )/(Double)( num_data );
cos_tbl[n] = cos( arg );
sin_tbl[n] = sin( arg );
}
}
n_half = num_data >> 1;
// for ( int n = 1; n < num_data; n = n * 2 )
for n in sequence( first: 1, next: { $0 * 2 }).prefix( while: { $0 < num_data })
{
n_half2 = n_half * 2;
// for ( int m = 0; m < num_data; m = m + n_half2 )
for m in sequence( first: 0, next: { $0 + n_half2 }).prefix( while: { $0 < num_data })
{
var w = 0;
// for ( int j = m; j < m + n_half; j++ )
for j in m ..< m + n_half
{
k = j + n_half;
tmpReJ = data_re[j];
tmpImJ = data_im[j];
tmpReK = data_re[k];
tmpImK = data_im[k];
newReJ = tmpReJ + tmpReK;
newImJ = tmpImJ + tmpImK;
tmpReJ = tmpReJ - tmpReK;
tmpImJ = tmpImJ - tmpImK;
newReK = tmpReJ * cos_tbl[w] - tmpImJ * sin_tbl[w];
newImK = tmpReJ * sin_tbl[w] + tmpImJ * cos_tbl[w];
data_re[j] = newReJ;
data_im[j] = newImJ;
data_re[k] = newReK;
data_im[k] = newImK;
w = w + n;
}
}
n_half = n_half / 2;
}
let _ = bit_reverse( &data_re );
let _ = bit_reverse( &data_im );
if ( mode == MyFourierObject.MODE_TIME_TO_FREQ )
{
// Time to Freq.
// nop.
}
else
{
// Freq to Time.
// for ( int n = 0; n < num_data; n++ )
for n in 0 ..< num_data
{
data_re[n] = (Double)( data_re[n] )/(Double)( num_data );
data_im[n] = (Double)( data_im[n] )/(Double)( num_data );
}
}
return 0;
}
}
こちらに vDSP を使ったコードの紹介記事があります。

