タップした3点を通過する2次曲線を描画する
任意の3点から2次曲線を描画してみます。
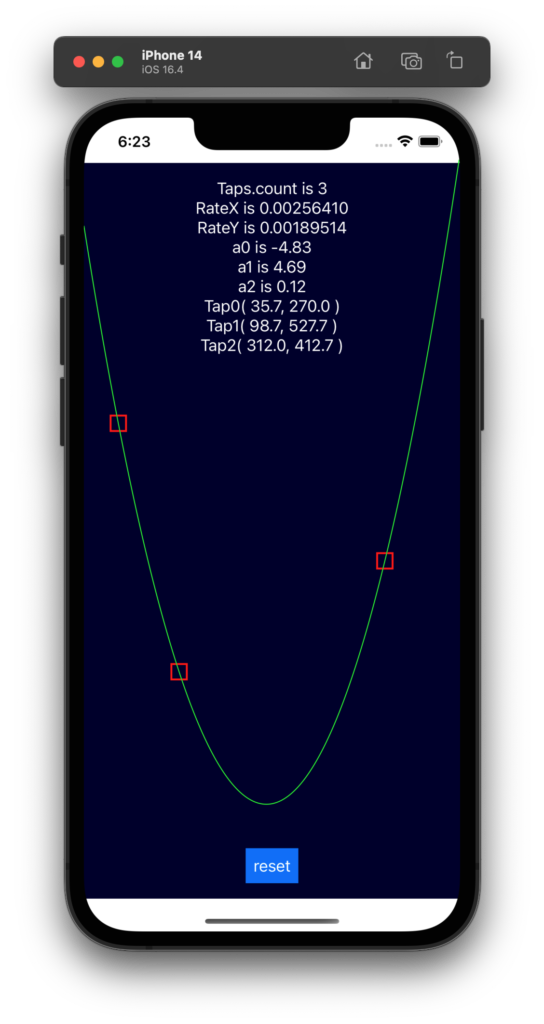
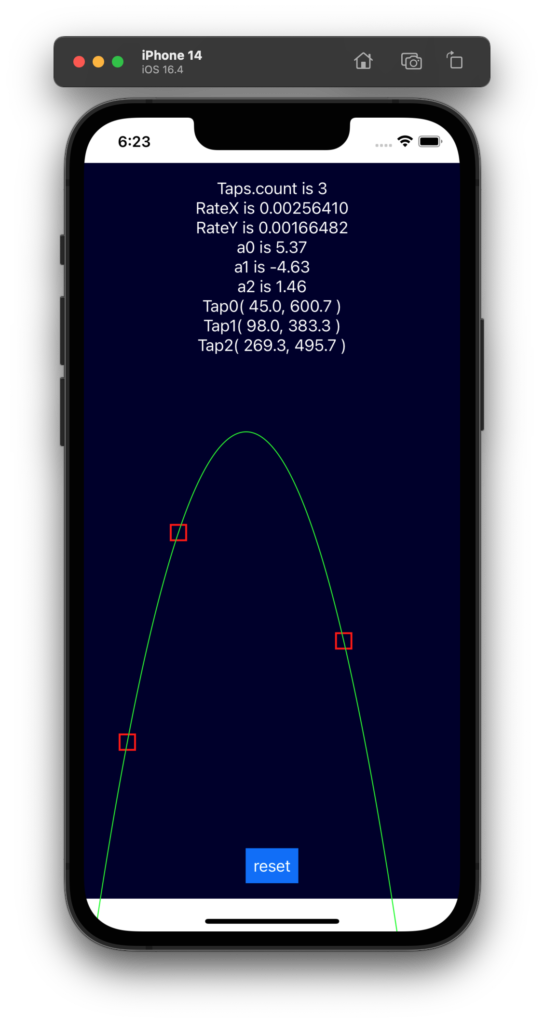
下記のような実行画面になります。サンプルソースをビルドしてランさせて3点をタップします。タップした座標のオンラインを通る波形を描画します。画面の幅、具体的には GeometryReader でよみとった ZStack の幅を、データの x 方向のデータ個数とし、それに応じた f(x) の値を描画します。
2次曲線は f(x) = a0 * x ^2 + a1 * x + a2 という3つの係数で決定されます。
ここでは 3 * 3 の逆行列を使って a0, a1, a2 の係数をもとめています。
3 * 3 の行列の逆行列を算出する方法は下記の2種類があります。
(1) 余因子行列を用いた公式をつかって算出する方法
(2) ガウスの掃出し法をつかって算出する方法
の2種類がありますが、3 * 3 の逆行列だと (1) を使う方法が簡単です。もっと高次の行列の逆行列をもとめるには (2) の方法しかありません。
下記が実行のためのコードです。簡単に解説します。
特に難しいところはないのですが、いちばん重要なのは、逆行列を算出するときに与える数値を、座標値そのまま与えてはいけないということです。
内部の演算で2乗や、その2乗した値を、3項かけたりするので、場合によってはやたらと大きな値になったりします。そうすると演算誤差がおおきくなってしまい適切な係数が得られない場合もあります。
ですので、それを避けるために x や f(x) の値は 0 〜 1.0 に正規化したものを与えてやり、計算後に正規化した操作の逆をしてやるのが定石です。
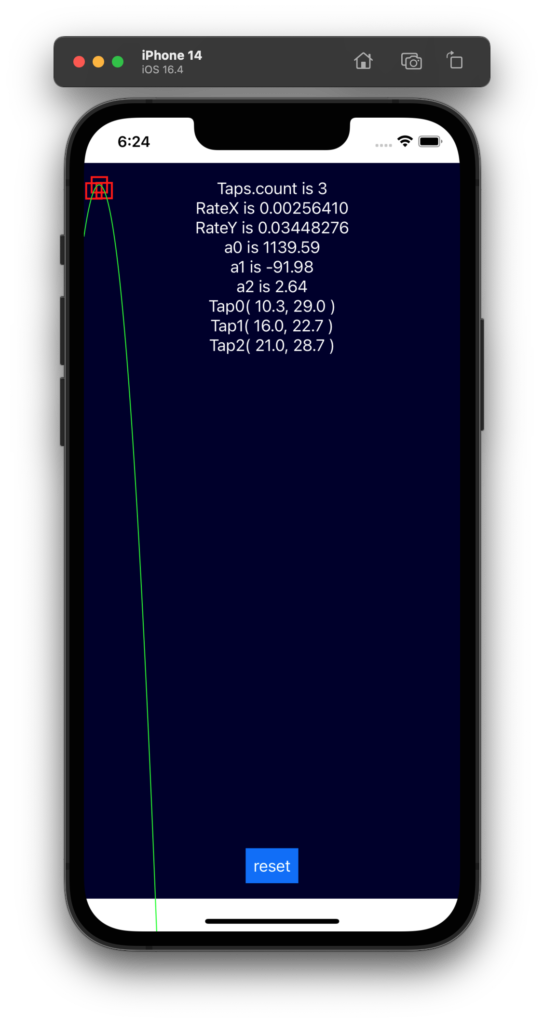
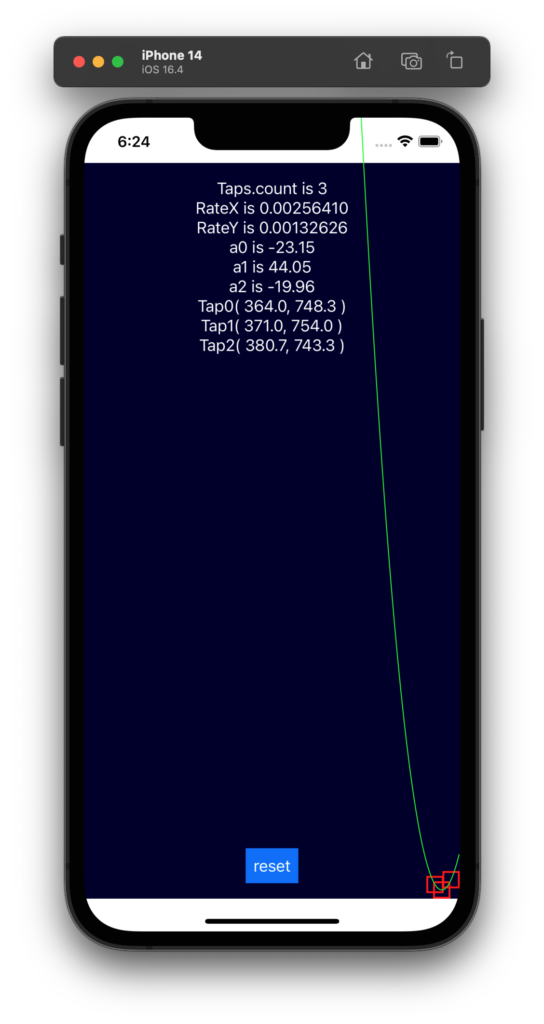
ここで、x は画像の幅で割り算することで 0 〜 1.0 に正規化します。つまり画面のいちばん左側が 0.0 で、いちばん右側が 1.0 です。f(x) は最大のY座標値で割り算することで 0 〜 1.0 に正規化します。こうすれば Fig. 3 や Fig. 4 のような極端な条件のときも正しく2次曲線を描画することができます。
ちなみに3点すべて違う座標でないと、未知数3の方程式が成立しないので、3つの係数を算出することはできません。
import SwiftUI
struct X_FX {
var x: Double
var fx: Double
}
struct ContentView: View {
@State var a0: Double = 0.0
@State var a1: Double = 0.0
@State var a2: Double = 0.0
@State var Taps = [CGPoint]()
@State var Data = [X_FX]()
let COLOR_BG = Color( red: 0.0, green: 0.0, blue: 0.2, opacity: 1.0 )
let COLOR_MARKER = Color( red: 1.0, green: 0.0, blue: 0.0, opacity: 1.0 )
let COLOR_WAVE = Color( red: 0.0, green: 1.0, blue: 0.0, opacity: 1.0 )
let COLOR_TEXT = Color( red: 1.0, green: 1.0, blue: 1.0, opacity: 1.0 )
@State var RateX: Double = 1.0
@State var RateY: Double = 1.0
let MARKER_WH = 16.0
var body: some View {
GeometryReader{
geom in
let geom_w = geom.size.width;
let geom_h = geom.size.height;
ZStack{
// 背景とタップジェスチャの動作.
Rectangle()
.foregroundColor( COLOR_BG )
.frame( width: geom_w, height: geom_h )
.onTapGesture {
tap in
// 与える座標が3点になるまで追加する.
if ( Taps.count < 3 )
{
let element = CGPoint( x: tap.x, y: tap.y )
Taps.append( element )
}
// 与える座標が3点になったら計算をする.
if ( Taps.count >= 3 )
{
// 与える座標は、x, f(x) の存在範囲がともに 0.0 〜 1.0 になるように正規化する.
let tmp_x0 = Taps[0].x
let tmp_x1 = Taps[1].x
let tmp_x2 = Taps[2].x
let tmp_fx0 = Taps[0].y
let tmp_fx1 = Taps[1].y
let tmp_fx2 = Taps[2].y
// 正規化するために f(x) の最大値を取得する.
var max_fx = 0.0
let _ = GetMaxValue( &max_fx, tmp_fx0, tmp_fx1, tmp_fx2 )
// X座標の正規化はデータ個数から実施、Y座標の正規化はf(x)の最大値から実施.
RateX = 1.0 / Double( Data.count )
RateY = 1.0 / max_fx
// 0.0〜1.0に正規化された座標をつかって2次曲線の3つの係数を取得する.
let x0 = tmp_x0 * RateX
let x1 = tmp_x1 * RateX
let x2 = tmp_x2 * RateX
let fx0 = tmp_fx0 * RateY
let fx1 = tmp_fx1 * RateY
let fx2 = tmp_fx2 * RateY
let _ = GetCoef_a0_a1_a2( &a0, &a1, &a2, x0, fx0, x1, fx1, x2, fx2 )
// 得られた3つの係数から全データを計算する.
for i in 0 ..< Data.count {
let x: Double = Double(i) * RateX // 0.0 〜 1.0
let fx: Double = (( a0 * x * x ) + ( a1 * x ) + ( a2 ))
Data[i].x = x
Data[i].fx = fx
}
}
}
// タップした座標をマーカーとして描画するパス.
Path{
path in
for n in 0 ..< Taps.count {
let off = MARKER_WH * 0.5
let x = Taps[n].x - off
let y = Taps[n].y - off
let rect = CGRect( x: x, y: y, width: MARKER_WH, height: MARKER_WH )
path.addRect( rect )
}
}
.stroke( COLOR_MARKER, lineWidth: 2.0 )
// 2次曲線を描画するパス.
Path{
path in
if Data.count > 0 {
if (( RateX != 0.0 ) && ( RateY != 0.0 )) {
var x = 0.0
var fx = 0.0
// 正規化されたデータから実際の座標データに戻す.
x = Data[0].x / RateX
fx = Data[0].fx / RateY
path.move( to: CGPoint( x: x, y: fx ))
for i in 0 ..< Data.count {
// 正規化されたデータから実際の座標データに戻す.
x = Data[i].x / RateX
fx = Data[i].fx / RateY
path.addLine( to: CGPoint( x: x, y: fx ))
}
}
}
}
.stroke( COLOR_WAVE, lineWidth: 1.0 )
VStack {
// タップした回数と2次曲線の係数 a0, a1, a2 を表示するテキスト.
VStack {
// タップした座標の個数.
Text( String( format: "Taps.count is %d", Taps.count ) )
.foregroundColor( COLOR_TEXT )
// 座標を正規化するレート.
Text( String( format: "RateX is %.8f", RateX ) )
.foregroundColor( COLOR_TEXT )
Text( String( format: "RateY is %.8f", RateY ) )
.foregroundColor( COLOR_TEXT )
// 2次曲線の3つの係数.
Text( String( format: "a0 is %.2f", a0 ) )
.foregroundColor( COLOR_TEXT )
Text( String( format: "a1 is %.2f", a1 ) )
.foregroundColor( COLOR_TEXT )
Text( String( format: "a2 is %.2f", a2 ) )
.foregroundColor( COLOR_TEXT )
// タップされた実際の座標値を示す.
if Taps.count == 3 {
Text( String( format: "Tap0( %.1f, %.1f )", Taps[0].x, Taps[0].y ) )
.foregroundColor( COLOR_TEXT )
Text( String( format: "Tap1( %.1f, %.1f )", Taps[1].x, Taps[1].y ) )
.foregroundColor( COLOR_TEXT )
Text( String( format: "Tap2( %.1f, %.1f )", Taps[2].x, Taps[2].y ) )
.foregroundColor( COLOR_TEXT )
}
}
.frame( maxWidth: .infinity, maxHeight: .infinity, alignment: .top )
.padding( .top )
// タップした座標と波形データをリセットするボタン.
Button( action: {
// タップした座標をリセットする.
Taps.removeAll();
// データもゼロリセットする.
for n in 0 ..< Data.count {
Data[n].x = 0.0
Data[n].fx = 0.0
}
}){
Text( "reset" )
.foregroundColor( .white )
}
.padding( 8.0 )
.background( .blue )
.frame( maxWidth: .infinity, maxHeight: .infinity, alignment: .bottom )
.padding( .bottom )
}
}
.onAppear(){
// 画面の幅のぶんだけ波形データの個数を確保する.
let loop = Int( geom_w )
for _ in 0 ..< loop {
let element = X_FX( x: 0.0, fx: 0.0 )
Data.append( element )
}
}
}
}
func GetMaxValue( _ want: inout Double, _ v0: Double, _ v1: Double, _ v2: Double )->Bool
{
let arr = [ v0, v1, v2 ]
want = arr.max()!
return true
}
// 3点をオンラインで通過する2次曲線の係数を取得するメソッド.
func GetCoef_a0_a1_a2(
_ a0: inout Double,
_ a1: inout Double,
_ a2: inout Double,
_ x0: Double, _ fx0: Double,
_ x1: Double, _ fx1: Double,
_ x2: Double, _ fx2: Double
) -> Bool
{
// エクセルで計算した理想的な答え.
// ( 19, 0.1 ) ( 20, 1.0 ) ( 21, 0.9 )
// | 19*19, 19, 1 ||a0| |0.1|
// | 20*20, 20, 1 ||a1| = |1.0|
// | 21*21, 21, 1 ||a2| |0.9|
// a0 = -0.5
// a1 = +20.4
// a2 = -207.0
// f(x) = ( a0 * x * x ) + ( a1 * x ) + ( a2 ).
let a11 = x0 * x0; let a12 = x0; let a13 = 1.0;
let a21 = x1 * x1; let a22 = x1; let a23 = 1.0;
let a31 = x2 * x2; let a32 = x2; let a33 = 1.0;
let tmp0 = ( a11 * a22 * a33 );
let tmp1 = ( a12 * a23 * a31 );
let tmp2 = ( a13 * a21 * a32 );
let tmp3 = ( a13 * a22 * a31 );
let tmp4 = ( a12 * a21 * a33 );
let tmp5 = ( a11 * a23 * a32 );
let btm = tmp0 + tmp1 + tmp2 - tmp3 - tmp4 - tmp5;
if ( btm == 0.0 ) {
return false;
}
let k = Double( 1.0 )/Double( btm );
let A11 = +(( a22 * a33 ) - ( a23 * a32 )); let A12 = -(( a12 * a33 ) - ( a13 * a32 )); let A13 = +(( a12 * a23 ) - ( a13 * a22 ));
let A21 = -(( a21 * a33 ) - ( a23 * a31 )); let A22 = +(( a11 * a33 ) - ( a13 * a31 )); let A23 = -(( a11 * a23 ) - ( a13 * a21 ));
let A31 = +(( a21 * a32 ) - ( a22 * a31 )); let A32 = -(( a11 * a32 ) - ( a12 * a31 )); let A33 = +(( a11 * a22 ) - ( a12 * a21 ));
// ここが 3 * 3 逆行列.
let M11 = k * A11; let M12 = k * A12; let M13 = k * A13;
let M21 = k * A21; let M22 = k * A22; let M23 = k * A23;
let M31 = k * A31; let M32 = k * A32; let M33 = k * A33;
// 3 * 3 行列、3 * 1 行列の掛け算.
a0 = ( M11 * fx0 ) + ( M12 * fx1 ) + ( M13 * fx2 );
a1 = ( M21 * fx0 ) + ( M22 * fx1 ) + ( M23 * fx2 );
a2 = ( M31 * fx0 ) + ( M32 * fx1 ) + ( M33 * fx2 );
return true
}
}
struct ContentView_Previews: PreviewProvider {
static var previews: some View {
ContentView()
}
}
